오일러 지표에 관한 문제를 처음으로 풀어보았다. 오일러 지표 문제라는 걸 몰랐으면 못 풀었을 거 같다.
1. 풀이
문제에서 요구하는 것은 되게 간단하다 어떤 알파벳들로 이루어진 필드가 있고 어떤 쿼리\((x1,\;y1,\;x2,\;y2)\) 가 주어지는 데 이 범위에서 같은 색깔로 이루어진 컴포넌트를 구하라는 것이다.
무식하게 생각하면 각 쿼리에 대해 BFS를 해주면 되지만 여기서 딱히 최적화할 여지가 없다. 여기서 오일러 지표를 사용한다는 걸 알면 문제에서 생각할 여지가 생긴다.
먼저 평면 그래프에서 오일러 지표 공식은 아래와 같이 성립한다. \(v−e+f=c+1\)
이 성립한다. 필드는 아래와 같이 그래프로 해석해볼 수 있다.
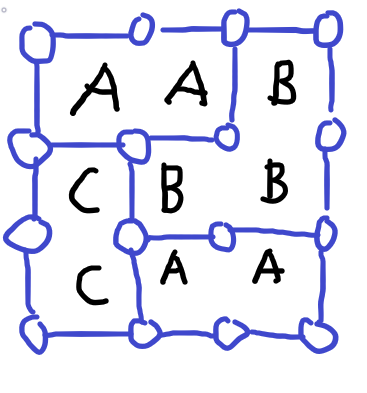
여기서 오일러 지표 공식을 사용하면 \(f−1\)(오일러 지표 공식에서는 바깥면도 고려하기 때문에 1을 빼줘야 된다.)값을 보면 올바른 답을 출력한다. 그리고 우리가 구하고자 하는 것은 \(f\)(면)이기 때문에 \(v\)(정점), \(e\)(간선), \(c\)(컴포넌트)를 알아야 된다. 각 정점과 간선은 BFS로 잘 이어 줄 수 있고, \(v,\;e\)는 구간 합으로 빠르게 구해줄 수 있다. 하지만 \(c\)를 구하는 것이 살짝 난감한데, 그래프 탐색을 하면서 컴포넌트에서 대표하는 정점을 하나를 잡고 구간합을 만든다. 그리고 컴포넌트들의 정점에 대해 대표하는 정점을 가르키는 배열을 만든다. 그리고 구간합으로 개수를 구한다. 쿼리로 들어오는 부분의 외곽선은 반드시 이어지기 때문에 외곽선에 있는 정점들중 자신이 속한 컴포넌트의 대표 정점이 쿼리 구간안에 있다면 \(-1\) 해준다. 중복으로 오는 경우는 잘 처리해주면 된다. 이렇게 처리한다면 쿼리당 \(O(N+M)\)에 할 수 있으므로 문제는 \(O((N+M)Q)\)에 풀리게 된다.
2.소스 코드
#include <bits/stdc++.h>
using namespace std;
const int MAX = 1111;
typedef pair<int, int> pi;
#define x first
#define y second
char arr[MAX][MAX];
int psum[MAX][MAX];
int comp[MAX][MAX];
pi topos[MAX][MAX];
vector<pi> V[MAX][MAX];
int dx[4] = { 1, 0, -1, 0 };
int dy[4] = { 0, 1, -1, 0 };
vector<vector<bool>> vit(MAX, vector<bool>(MAX));
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int n, m, q; cin >> n >> m >> q;
for (int i = 1; i <= n; i++) {
string str; cin >> str;
for (int j = 1; j <= m; j++) arr[i][j] = str[j-1];
}
for (int i = 2; i <= n + 1; i++) {
V[i - 1][1].push_back({i, 1});
V[i][1].push_back({i-1, 1});
psum[i][1]++;
}
for (int i = 2; i <= m + 1; i++) {
V[1][i].push_back({1, i-1});
V[1][i-1].push_back({1, i});
psum[1][i]++;
}
for(int i=1; i <= n; i++)
for (int j = 1; j <= m; j++) {
for (int k = 0; k < 2; k++) {
int nx = i + dx[k], ny = j + dy[k];
if (arr[i][j] != arr[nx][ny]) {
psum[i + 1][j + 1]++;
V[i+1][j+1].push_back({nx, ny});
V[nx][ny].push_back({i+1, j+1});
}
}
}
for (int i = 1; i <= n+1; i++) {
for (int j = 1; j <= m+1; j++) {
if (vit[i][j]) continue;
vit[i][j] = true;
queue<pi> q; q.push({i, j});
comp[i][j]++;
while (!q.empty()) {
pi top = q.front(); q.pop();
topos[top.x][top.y] = { i, j };
for (pi& w : V[top.x][top.y]) {
int nx = w.x, ny = w.y;
if (nx < 1 || ny < 1 || nx > n + 1 || ny > m + 1) continue;
if (vit[nx][ny]) continue;
vit[nx][ny] = true;
q.push({ nx, ny });
}
}
}
}
for (int i = 1; i <= n + 1; i++)
for (int j = 1; j <= m + 1; j++) {
psum[i][j] += psum[i - 1][j] + psum[i][j - 1] - psum[i - 1][j - 1];
comp[i][j] += comp[i - 1][j] + comp[i][j - 1] - comp[i - 1][j - 1];
}
while (q--) {
int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
int v = abs(x2 - x1 + 2) * abs(y2 - y1 + 2);
int e = psum[x2+1][y2+1] - psum[x1][y2+1] - psum[x2+1][y1] + psum[x1][y1];
e += abs(x2-x1+1)+abs(y2-y1+1);
int c = comp[x2 + 1][y2 + 1] - comp[x1-1][y2 + 1] - comp[x2 + 1][y1-1] + comp[x1-1][y1-1];
map<pi, bool> mp;
for (int i = x1; i <= x2+1; i++) {
if (i <= x2 && arr[i][y2] == arr[i][y2 + 1]) e++;
pi pos = topos[i][y1];
if (x1 <= pos.x && pos.x <= x2 + 1 && y1 <= pos.y && pos.y <= y2 + 1) {
if (!mp[pos]) c--,mp[pos] = true;
}
pos = topos[i][y2+1];
if (x1 <= pos.x && pos.x <= x2 + 1 && y1 <= pos.y && pos.y <= y2 + 1) {
if (!mp[pos]) c--, mp[pos] = true;
}
}
for (int i = y1; i <= y2+1; i++) {
if (i <= y2 && arr[x2][i] == arr[x2 + 1][i]) e++;
pi pos = topos[x1][i];
if (x1 <= pos.x && pos.x <= x2 + 1 && y1 <= pos.y && pos.y <= y2 + 1) {
if (!mp[pos]) c--, mp[pos] = true;
}
pos = topos[x2+1][i];
if (x1 <= pos.x && pos.x <= x2 + 1 && y1 <= pos.y && pos.y <= y2 + 1) {
if (!mp[pos]) c--, mp[pos] = true;
}
}
c++;
cout << c+e-v << "\n";
}
return 0;
}'PS > 백준' 카테고리의 다른 글
| [백준 22349] 가장 긴 공통 괄호 문자열 (0) | 2021.12.11 |
|---|---|
| [백준 22348] 헬기 착륙장 (0) | 2021.11.30 |
| [백준 15555] Dango Maker (0) | 2021.11.30 |
| [백준 17528] Two Machines (0) | 2021.11.30 |
| [백준 10272] 현상금 사냥꾼 김정은 (0) | 2021.11.30 |
![[백준 20966] Paint by Letters](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fb4hNCT%2FbtrmCCxxItc%2FAQnjQ64yQuikL9tdy1koWK%2Fimg.png)